- Fit a logistic regression model using all but the i-th observation to predict Direction using Lag1 and Lag2 .
- Compute the posterior probability of the market moving up for the i-th observation.
- Use the posterior probability for the i-th observation in order to predict whether or not the market moves up.
- Determine whether or not an error was made in predicting the direction for the i-th observation. If an error was made, then indicate this as a 1, and otherwise indicate it as a 0.
prediction_errors rep(NA, nrow(Weekly)) for (i in 1:nrow(Weekly)) glm(Direction ~ Lag1 + Lag2, data = Weekly[-i,], family = binomial) predicted_direction predict_glm_direction(logit_model, Weekly[i,]) prediction_errors[i] ifelse(predicted_direction != Weekly$Direction[i], 1, 0) >- Take the average of the n numbers obtained in (d)iv in order to obtain the LOOCV estimate for the test error. Comment on the results.
mean(prediction_errors)[1] 0.4499541LOOCV estimates a test error rate of 0.4499541.
4.2.2 Exercise
In this exercise, we will predict the number of applications received using the other variables in the College data set.
- Split the data set into a training set and a test set.
Load and split the College data.
# split the dataset into training and test set with the split_ratio. Optionally set the random seed before splitting # returns a list of two elements: # - first element is the training subset # - second elemet is the test subset sample_split function(dataset, split_ratio, seed = NULL) < set.seed(seed) train_subset sample(nrow(dataset) * split_ratio) return(list( train = dataset[train_subset, ], test = dataset[-train_subset, ] )) > college_split sample_split(College, 0.7, seed = 12345)- Fit a linear model using least squares on the training set, and report the test error obtained.
ols_model lm(Apps ~ . , data = college_split$train) ols_predictions predict(ols_model, college_split$test)Since we need to calculate the MSE throughout this exercise, let’s write a function to do that.
calc_rmse function(y, y_hat) < return(sqrt(mean((y - y_hat)^2))) >Now we can calculate the MSE for the OLS model
ols_rmse calc_rmse(college_split$test$Apps, ols_predictions)Test RMSE for OLS is: 1188.832
- Fit a ridge regression model on the training set, with \(\lambda\) chosen by cross-validation. Report the test error obtained.
Pick \(\lambda\) using training subset and report error on test subset
train_matrix model.matrix(Apps ~ . , data = college_split$train) test_matrix model.matrix(Apps ~ . , data = college_split$test) grid 10 ^ seq(4, -2, length = 100) ridge_model cv.glmnet(train_matrix, college_split$train$Apps, alpha = 0, lambda = grid, thresh = 1e-12) ridge_predictions predict(ridge_model, test_matrix, s = ridge_model$lambda.min) ridge_rmse calc_rmse(college_split$test$Apps, ridge_predictions)Test RMSE for ridge model is: 1188.8145824
- Fit a lasso model on the training set, with \(\lambda\) chosen by cross-validation. Report the test error obtained, along with the number of non-zero coefficient estimates.
Pick \(\lambda\) using training subset and report error on test subset
lasso_model cv.glmnet(train_matrix, college_split$train$Apps, alpha = 1, lambda = grid, thresh = 1e-12) lasso_predictions predict(lasso_model, test_matrix, s = lasso_model$lambda.min) lasso_rmse calc_rmse(college_split$test$Apps, lasso_predictions)Test RMSE for lasso model is: 1188.7994726
predict(lasso_model, s = lasso_model$lambda.min, type = "coefficients")19 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) -601.38112596 (Intercept) . PrivateYes -321.41076249 Accept 1.70685797 Enroll -1.35810665 Top10perc 45.45111099 Top25perc -15.88692306 F.Undergrad 0.09983028 P.Undergrad 0.01567394 Outstate -0.09222852 Room.Board 0.11816525 Books -0.04056782 Personal 0.05792203 PhD -5.56419852 Terminal -5.43103094 S.F.Ratio 21.59623616 perc.alumni 1.87814752 Expend 0.10806715 Grad.Rate 8.13596816- Fit a PCR model on the training set, with \(M\) chosen by cross-validation. Report the test error obtained, along with the value of \(M\) selected by cross-validation.
pcr_model pcr(Apps ~ . , data = college_split$train, scale = TRUE, validation = "CV") validationplot(pcr_model, val.type = "MSEP")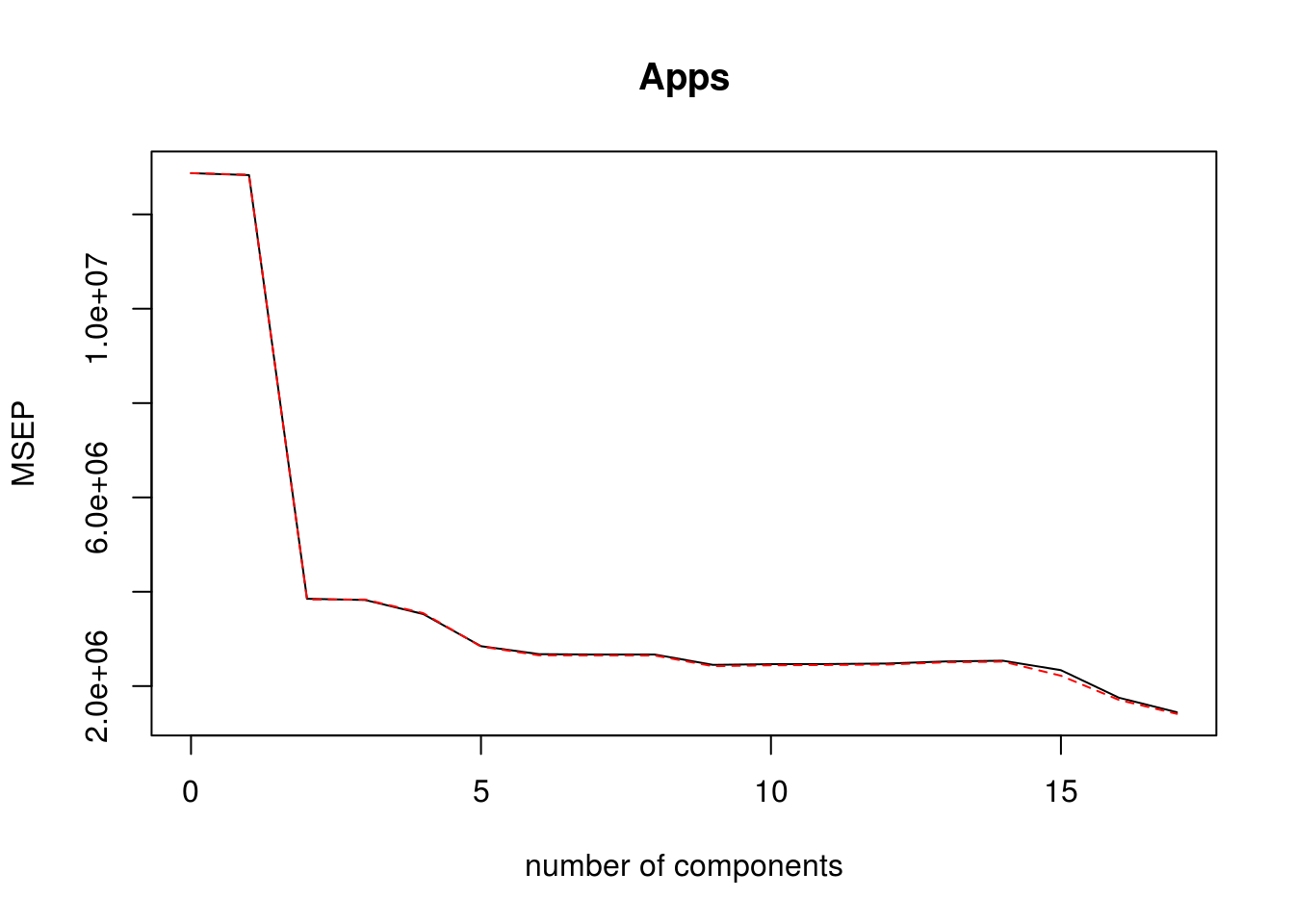
pcr_predictions predict(pcr_model, college_split$test, ncomp = 10) pcr_rmse calc_rmse(college_split$test$Apps, pcr_predictions)Test RMSE for PCR model is: 1556.8207088
- Fit a PLS model on the training set, with \(M\) chosen by cross-validation. Report the test error obtained, along with the value of \(M\) selected by cross-validation.
pls_model plsr(Apps ~ . , data = college_split$train, scale = TRUE, validation = "CV") validationplot(pls_model, val.type = "MSEP")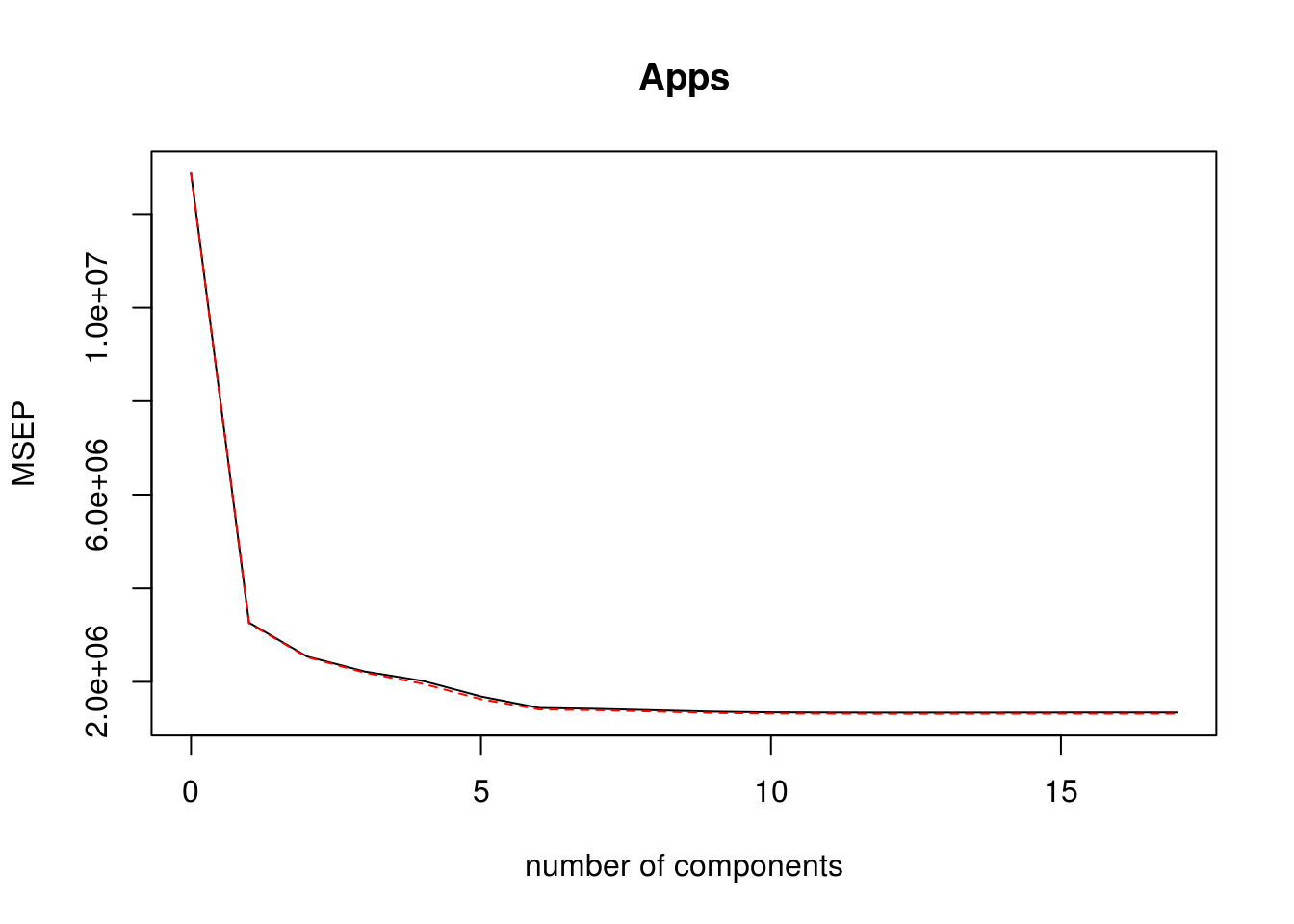
pls_predictions predict(pls_model, college_split$test, ncomp = 10) pls_rmse calc_rmse(college_split$test$Apps, pls_predictions)Test RMSE for PLS model is: 1178.3609154
- Comment on the results obtained. How accurately can we predict the number of college applications received? Is there much difference among the test errors resulting from these five approaches?
Let’s write a function to compute the \(R^2\) so we can compare the fit for various models. Recall that the \(R^2\) is given by:
calc_r2 function(y, y_hat) mean(y) rss sum((y - y_hat)^2) tss sum((y - y_bar)^2) return(1 - (rss / tss)) >Results for OLS, Lasso, Ridge are comparable. Lasso reduces the \(F.Undergrad\) and \(Books\) variables to zero and shrinks coefficients of other variables. Here are the test \(R^2\) for all models.
ols_r2 calc_r2(college_split$test$Apps, ols_predictions) ridge_r2 calc_r2(college_split$test$Apps, ridge_predictions) lasso_r2 calc_r2(college_split$test$Apps, lasso_predictions) pcr_r2 calc_r2(college_split$test$Apps, pcr_predictions) pls_r2 calc_r2(college_split$test$Apps, pls_predictions) barplot(c(ols_r2, ridge_r2, lasso_r2, pcr_r2, pls_r2), names.arg = c("OLS", "Ridge", "Lasso", "PCR", "PLS"))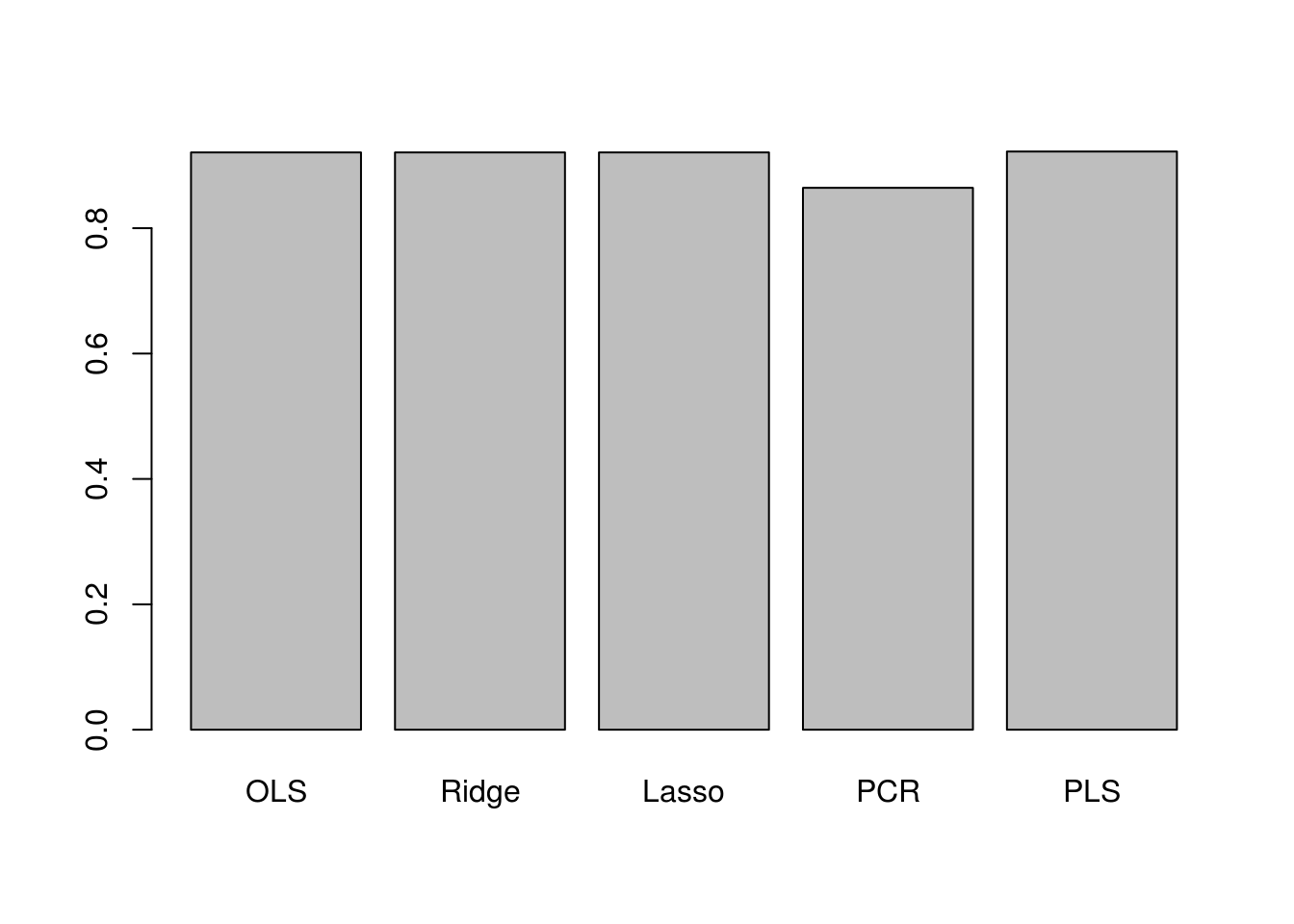
The plot shows that test \(R^2\) for all models except PCR are around 0.9, with PLS having slightly higher test \(R^2\) than others. PCR has a smaller test \(R^2\) of less than 0.8. All models except PCR predict college applications with high accuracy.
4.2.3 Exercise
We will now try to predict per capita crime rate in the Boston data set.
- Try out some of the regression methods explored in this chapter, such as best subset selection, the lasso, ridge regression, and PCR. Present and discuss results for the approaches that you consider.
Best subset selection
We need a function for getting predictions from a regsubsets model.
predict.regsubsets function(object, newdata, id, . ) as.formula(object$call[[2]]) model_matrix model.matrix(formula, newdata) coefi coef(object, id = id) model_matrix[, names(coefi)] %*% coefi >Now run K-fold cross-validation
set.seed(12345) k 10 p ncol(Boston)-1 folds sample(rep(1:k, length = nrow(Boston))) cv_errors matrix(NA, k, p) for (i in 1:k) regsubsets(crim ~ . , data = Boston[folds!=i,], nvmax = p) for (j in 1:p) predict(best_fit, Boston[folds==i, ], id = j) cv_errors[i,j] mean((Boston$crim[folds==i] - prediction)^2) > > cv_rmse sqrt(apply(cv_errors, 2, mean)) plot(cv_rmse, type = "b")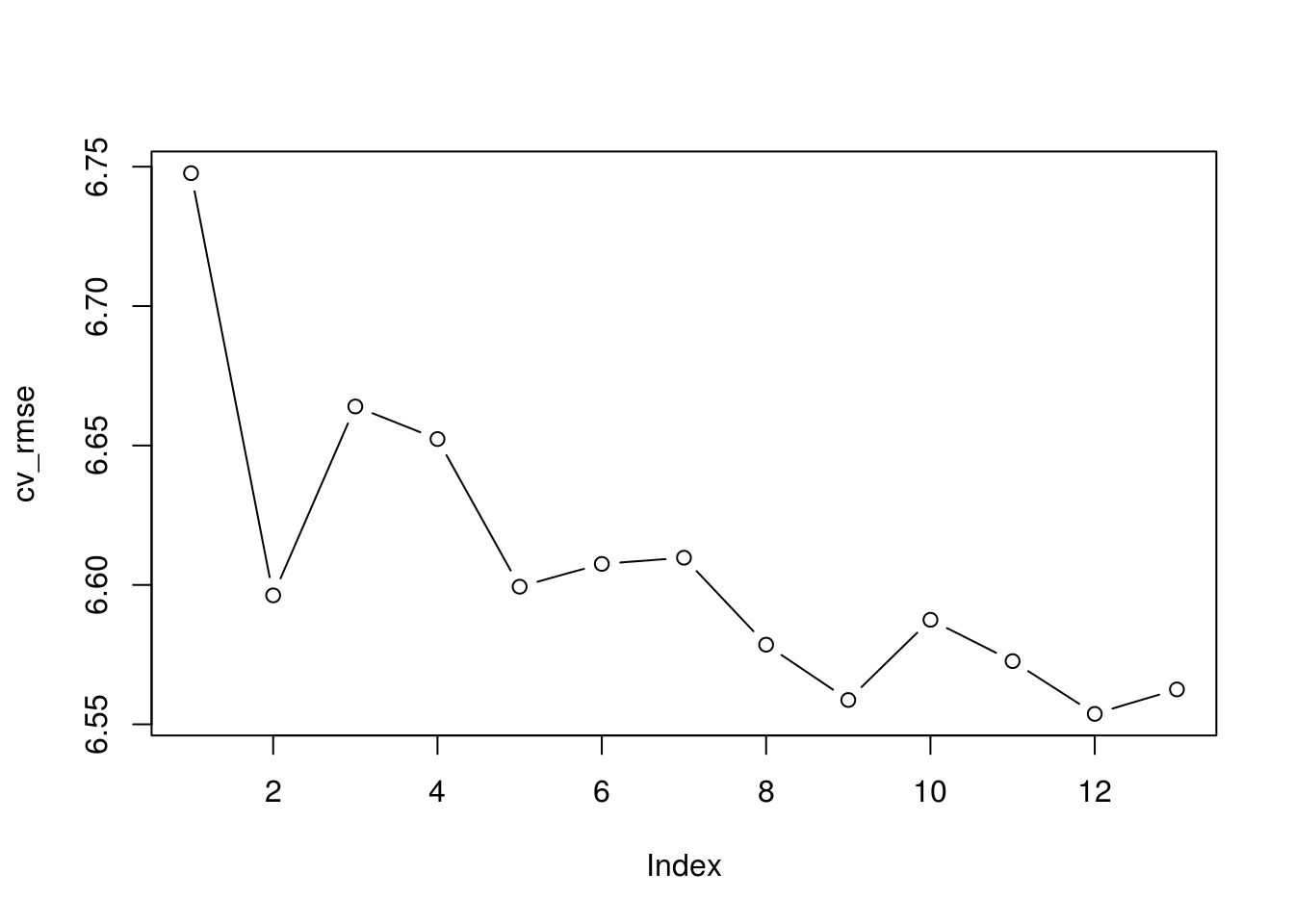
which.min(cv_rmse)[1] 12min(cv_rmse)[1] 6.55376Lasso
x model.matrix(crim ~ . -1, data = Boston) cv_lasso cv.glmnet(x, Boston$crim, type.measure = "mse", alpha = 1) plot(cv_lasso)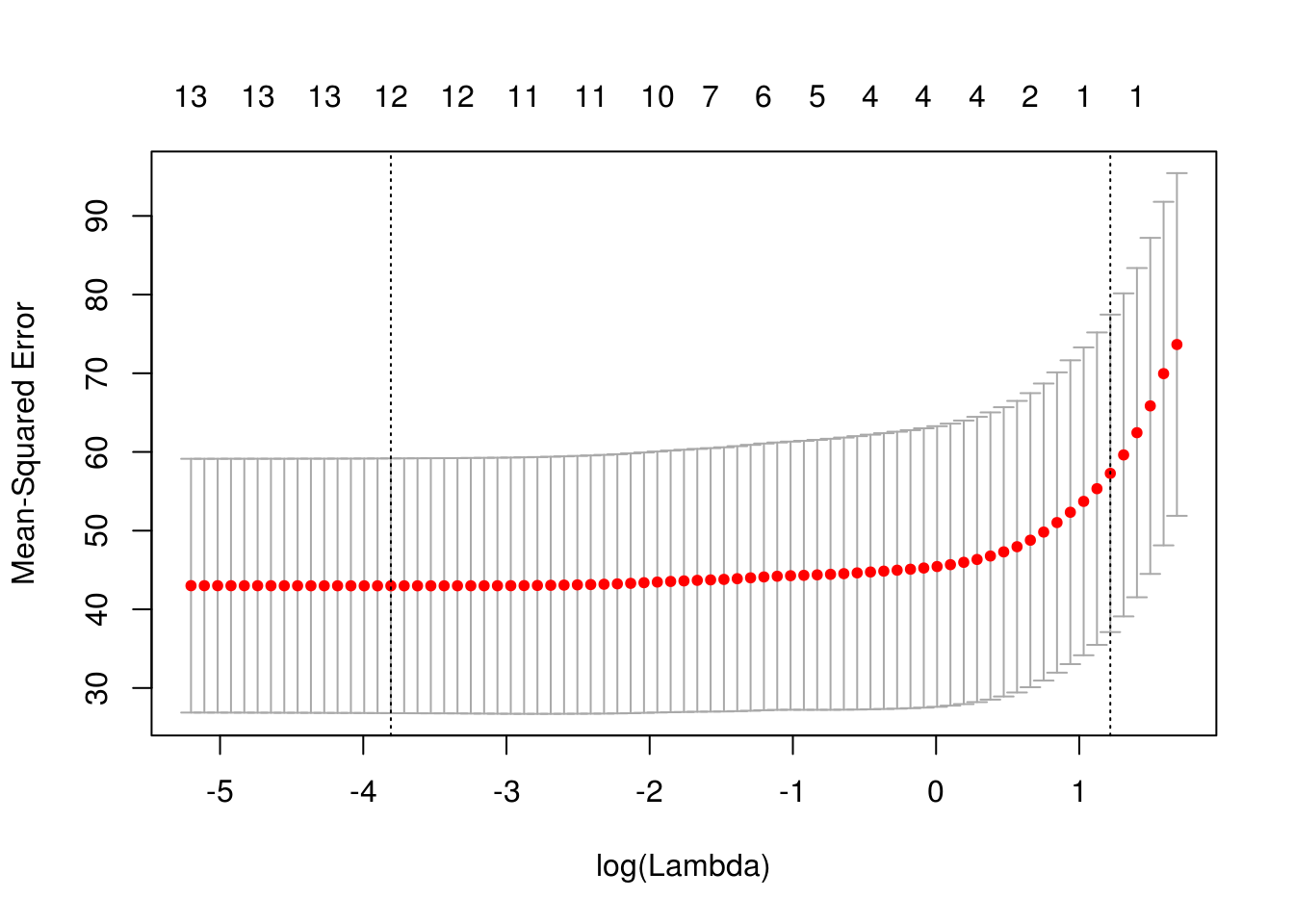
coef(cv_lasso)14 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 1.4186414 zn . indus . chas . nox . rm . age . dis . rad 0.2298449 tax . ptratio . black . lstat . medv . sqrt(cv_lasso$cvm[cv_lasso$lambda == cv_lasso$lambda.1se])[1] 7.568515Ridge regression
x model.matrix(crim ~ . -1, data = Boston) cv_ridge cv.glmnet(x, Boston$crim, type.measure = "mse", alpha = 0) plot(cv_ridge)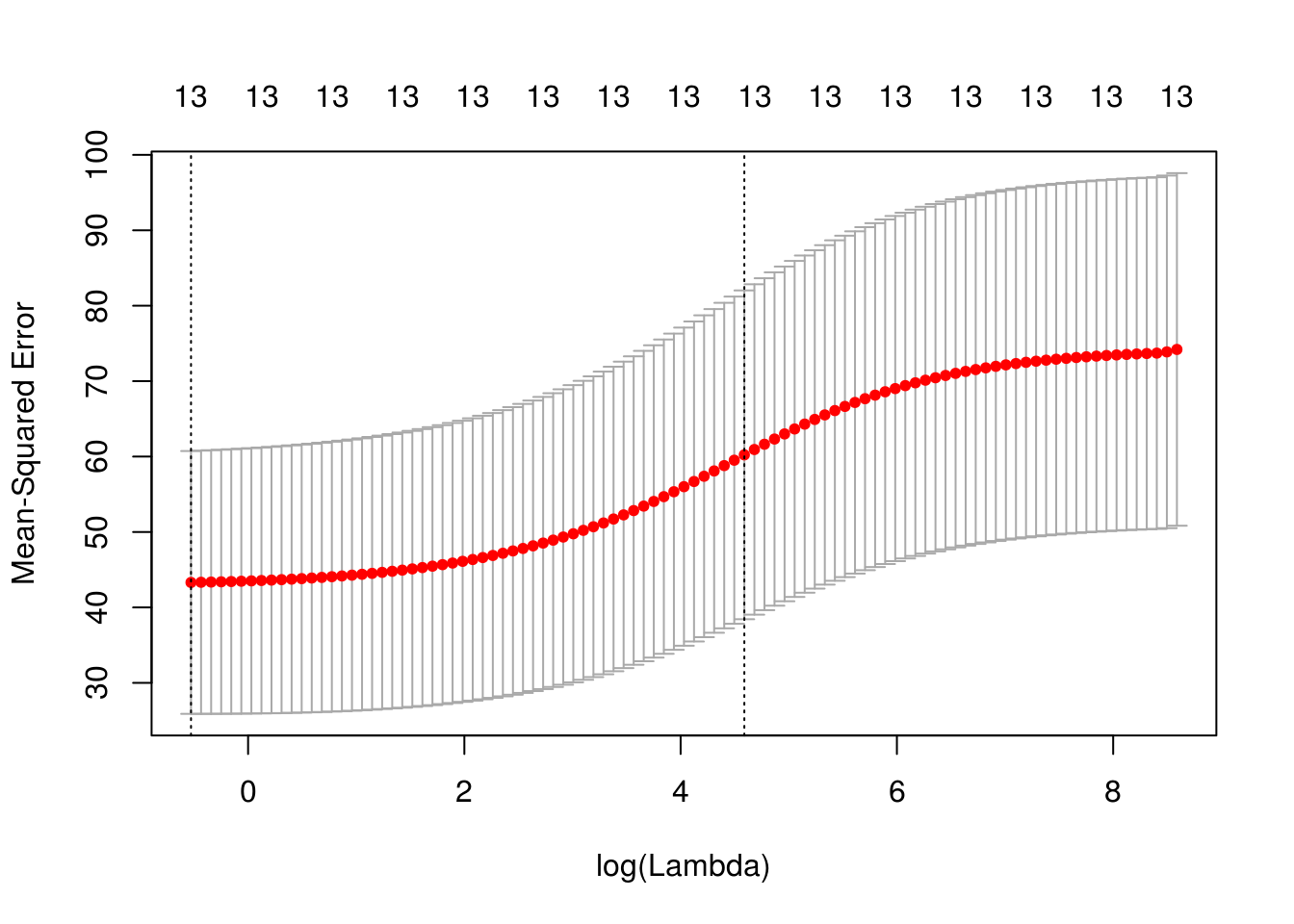
coef(cv_ridge)14 x 1 sparse Matrix of class "dgCMatrix" 1 (Intercept) 1.761587688 zn -0.002865786 indus 0.026514040 chas -0.142145708 nox 1.684835359 rm -0.130992458 age 0.005612849 dis -0.084630196 rad 0.039946869 tax 0.001830673 ptratio 0.063756646 black -0.002278831 lstat 0.031682619 medv -0.020839190sqrt(cv_ridge$cvm[cv_ridge$lambda == cv_ridge$lambda.1se])[1] 7.760891PCR
pcr_model pcr(crim ~ . , data = Boston, scale = TRUE, validation = "CV") summary(pcr_model)Data: X dimension: 506 13 Y dimension: 506 1 Fit method: svdpc Number of components considered: 13 VALIDATION: RMSEP Cross-validated using 10 random segments. (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps CV 8.61 7.270 7.278 6.832 6.824 6.855 6.908 adjCV 8.61 7.264 7.272 6.824 6.813 6.846 6.895 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps CV 6.901 6.770 6.800 6.795 6.811 6.784 6.705 adjCV 6.887 6.756 6.785 6.780 6.795 6.765 6.686 TRAINING: % variance explained 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps X 47.70 60.36 69.67 76.45 82.99 88.00 91.14 crim 30.69 30.87 39.27 39.61 39.61 39.86 40.14 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps X 93.45 95.40 97.04 98.46 99.52 100.0 crim 42.47 42.55 42.78 43.04 44.13 45.413 component PCR fit has lowest CV/adjCV RMSEP.
- Propose a model (or set of models) that seem to perform well on this data set, and justify your answer. Make sure that you are evaluating model performance using validation set error, cross-validation, or some other reasonable alternative, as opposed to using training error.
See above answer for cross-validated mean squared errors of selected models.
- Does your chosen model involve all of the features in the data set? Why or why not?
I would choose the 12 parameter best subset model because it had the best cross-validated RMSE, next to PCR, but it was simpler model than the 13 component PCR model.